هر تانسور از مرتبه ی n در فضایی m- بعدی، ساختاری ریاضیاتی است که n شاخص و
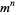
مولفه دارد که از قوانین تبدیلات مختصاتی پیروی می کند.
هر شاخص تانسور، فقط مقادیری در محدوده ی تعداد بعدهای فضای تعریفی اختیار می کند. با این حال دخالت ابعاد فضایی تا حدود زیادی در معادلات تانسوری نامربوط به نظر می رسد. (به استثنای حالت تنجش یافته ی تانسور کرونکر). تانسورها نوع عمومی تر اسکالرها ( که فاقد شاخص هستند) ،بردارها (که تنها دارای یک شاخص اند) و نیز متریک ها (که فقط دو شاخص دارند) می باشند که می توانند تعداد دلخواه شاخص اختیار کنند.
تانسورها بستر ریاضی مناسب و ساده ای را جهت فرمولبندی و حل مسائل متعدد در سیطره ی مباحث گوناگون فیزیک نظیر مکانیک سیالات و نسبیت عام فراهم می کنند.
نمادگذاری هر تانسور عیناْ شبیه به یک ماتریس است، (مثل 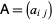 )، به جز اینکه یک تانسور مثلا
)، به جز اینکه یک تانسور مثلا 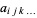 ،
، 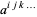 ،
، 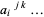 قدرت انتخاب هر تعداد شاخص دلخواه را شامل هستند. بعلاوه، یک تانسور از مرتبه ی
قدرت انتخاب هر تعداد شاخص دلخواه را شامل هستند. بعلاوه، یک تانسور از مرتبه ی  ،از نوع مختلط ـ شاخص یا به اصطلاح "مختلط"
،از نوع مختلط ـ شاخص یا به اصطلاح "مختلط"  ، تلفیقی از
، تلفیقی از  شاخص بالا یا "پادوردا (contravariant)" و
شاخص بالا یا "پادوردا (contravariant)" و  شاخص پایین "هم وردا (covariant)" می باشد. دقت کنید که مکان شاخص های پادوردا و هم وردا با یکدیگر فرق دارد که کوچکترین تفاوت میان جایدهی شاخص ها در یک تانسور چه در ترتیب و چه در بالا یا پایین بردن شاخص ها، منجر به ایجاد تانسور جدید و یا تغییر ساختمان ریاضی آن می گردد. برای مثال تانسور
شاخص پایین "هم وردا (covariant)" می باشد. دقت کنید که مکان شاخص های پادوردا و هم وردا با یکدیگر فرق دارد که کوچکترین تفاوت میان جایدهی شاخص ها در یک تانسور چه در ترتیب و چه در بالا یا پایین بردن شاخص ها، منجر به ایجاد تانسور جدید و یا تغییر ساختمان ریاضی آن می گردد. برای مثال تانسور  متمایز از شکل
متمایز از شکل  است.
است.
هنگامی که تانسور نسبت به تفاوت شاخص های پادوردا و هم وردا حساس باشد، تانسور حاصل از نوع عمومی خواهد بود. (در بحث ماتریس ها، یک ماتریس عمومی از جمع دو ماتریس پادمتقارن و متقارن به وجود می آمد که در اینجا نیز همین حالت برای تانسورها برقرار است). عدم تفاوت میان شاخص های هم وردا و پادوردا بیشتر در تانسورهای موردبحث در فضای اقلیدسی مانند تانسورهای دکارتی (Cartesian tensors) مطرح است.
تانسورهای تبدیل شونده از مرتبه ی صفر، اسکالر (scalars) نامیده می شوند که همانند تانسورهای مرتبه ی ۱ یعنی بردارها (vectors) تبدیل می شوند. در نمادنویسی تانسوری، هر بردار  به شکل
به شکل  نوشته می شود. به طوریکه i=1,...,m و ماتریس متناظر با آن گویای تانسوری از مرتبه ی (۱,۱) است که آن را به فرم
نوشته می شود. به طوریکه i=1,...,m و ماتریس متناظر با آن گویای تانسوری از مرتبه ی (۱,۱) است که آن را به فرم  می نویسیم.
می نویسیم.
می توان عملیات جبری و دیفرانسیل را بر روی تانسورها انجام داد (مانند تانسورهای متریک (metric tensors) و تانسور جایگشت (permutation tensor) یا نماد دلتای کرونکر) که قابلیت تعریف پذیری عملگرهای تانسوری را دارا هستند. [مانند مشتق هم وردا (semicolon derivatives)]. با جابجایی شاخص های هم وردا و پادوردا می توان به عبارات و تانسورهای ساده تری دست یافت که این کار شامل بالابردن (index raising) یا پایین آوردن شاخص ها (index lowering) یا به عبارت کلی بالانس شاخص ها ( index gymnastics) می باشد که آن ها را می توان با ضرب در تانسور متریک،  ،
،  ،
،  و ... به دست آورد.
و ... به دست آورد.
ادامه دارد...
منابع:
Abraham, R.; Marsden, J. E.; and Ratiu, T. S. Manifolds, Tensor Analysis, and Applications, 2nd ed. New York: Springer-Verlag, 1991.
Akivis, M. A. and Goldberg, V. V. An Introduction to Linear Algebra and Tensors. New York: Dover, 1972.
Arfken, G. "Tensor Analysis." Ch. 3 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 118-167, 1985.
Aris, R. Vectors, Tensors, and the Basic Equations of Fluid Mechanics. New York: Dover, 1989.
Bishop, R. and Goldberg, S. Tensor Analysis on Manifolds. New York: Dover, 1980.
Borisenko, A. I. and Tarpov, I. E. Vector and Tensor Analysis with Applications. New York: Dover, 1980.
Bott, R. and Tu, L. W. Differential Forms in Algebraic Topology. New York: Springer-Verlag, 199.
Cartan, É. The Theory of Spinors. New York: Dover, 1981.
Joshi, A. W. Matrices and Tensors in Physics, 3rd ed. Wiley, 1995.
Lass, H. Vector and Tensor Analysis. New York: McGraw-Hill, 1950.
Lawden, D. F. An Introduction to Tensor Calculus, Relativity, and Cosmology, 3rd ed. Chichester, England: Wiley, 1982.
Lovelock, D. and Rund, H. Tensors, Differential Forms, and Variational Principles. New York: Dover, 1989.
McConnell, A. J. Applications of Tensor Analysis. New York: Dover, 1947.
Nicolaescu, L. I. Lectures on the Geometry of Manifolds. Singapore: World Scientific, 1996.
Parker, L. and Christensen, S. M. MathTensor: A System for Doing Tensor Analysis by Computer. Reading, MA: Addison-Wesley, 1994.
Rashevskii, P. K. Riemann'sche Geometrie und Tensoranalysis. Berlin: Deutscher Verlag der Wissenschaften, 1959.
Simmonds, J. G. A Brief on Tensor Analysis, 2nd ed. New York: Springer-Verlag, 1994.
Sokolnikoff, I. S. Tensor Analysis: Theory and Applications to Geometry and Mechanics of Continua, 2nd ed. New York: Wiley, 1964.
Synge, J. L. and Schild, A. Tensor Calculus. New York: Dover, 1978.
Wrede, R. C. Introduction to Vector and Tensor Analysis. New York: Wiley, 1963
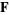 ، نمادگذاری به صورت
، نمادگذاری به صورت 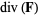 یا
یا 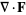 (در اینجا از نمادگذاری نوع دوم بهره خواهیم گرفت)، به وسیله حد انتگرال رویه ای (surface integral)
(در اینجا از نمادگذاری نوع دوم بهره خواهیم گرفت)، به وسیله حد انتگرال رویه ای (surface integral)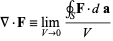
![]() روی رویه ی مرزی بینهایت کوچک بسته ای
روی رویه ی مرزی بینهایت کوچک بسته ای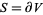 در اطراف عنصر حجمی
در اطراف عنصر حجمی![]() , را نشان می دهد، طوری که این رویه با استفاده از یک عملیات حدی به اندازه ی صفر برده شده است. بنابراین دیورژانس یک میدان برداری (vector field)، یک میدان اسکالر (scalar field) است. اگر
, را نشان می دهد، طوری که این رویه با استفاده از یک عملیات حدی به اندازه ی صفر برده شده است. بنابراین دیورژانس یک میدان برداری (vector field)، یک میدان اسکالر (scalar field) است. اگر ![]() ، آنگاه میدان یک میدان فاقد دیورژانس (divergenceless field) است. نماد
، آنگاه میدان یک میدان فاقد دیورژانس (divergenceless field) است. نماد 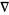 همچنین با نام عملگرهای "دل" (del) و یا "نابلا" (nabla) نیز شناخته می شود.
همچنین با نام عملگرهای "دل" (del) و یا "نابلا" (nabla) نیز شناخته می شود.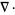 " §1.7 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 37-42, 1985.
" §1.7 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 37-42, 1985.  تانسور انحنای ریچی و
تانسور انحنای ریچی و  انحنای اسکالر یا نرده ای و بالاخره
انحنای اسکالر یا نرده ای و بالاخره  تانسور متریک را نشان می دهد. این تانسور تحت عمل دیورژانس هموردا همواره برابر صفر است. یعنی:
تانسور متریک را نشان می دهد. این تانسور تحت عمل دیورژانس هموردا همواره برابر صفر است. یعنی: ضرايب ارتباط (
ضرايب ارتباط ( . در چهار بعد این تانسور ۲۵۶ مولفه دارد. با استفاده از روابط تقارنی،
. در چهار بعد این تانسور ۲۵۶ مولفه دارد. با استفاده از روابط تقارنی، ساخت، برابرند با
ساخت، برابرند با ، که در آن دترمینان
، که در آن دترمینان  مخالف با صفر است. این تبدیل از دستگاه مختصات راست گوشه
مخالف با صفر است. این تبدیل از دستگاه مختصات راست گوشه  به دستگاه مختصات
به دستگاه مختصات




 تانسور لوی - سیویتا یا تانسور جایگشت (
تانسور لوی - سیویتا یا تانسور جایگشت ( می تواند به کمک حاصلضرب تانسوری فضای برداری (
می تواند به کمک حاصلضرب تانسوری فضای برداری ( میدان برداری (
میدان برداری ( میدان برداری دوگان نظیر یک شکلی ها (
میدان برداری دوگان نظیر یک شکلی ها ( - تانسوری بر روی خمینه ی (
- تانسوری بر روی خمینه ی ( بوده که
بوده که  کلاف مماس
کلاف مماس  دوگان آن می باشد. تانسورهای نوع
دوگان آن می باشد. تانسورهای نوع  یک فضای برداری (
یک فضای برداری ( نگاشت
نگاشت  را القاء می کند،
را القاء می کند،  است که با جابجایی ژاکوبی به طرف دیگر معادله حاصل شده است. این تعریف میتواند به دیگر ضرب های تانسوری (
است که با جابجایی ژاکوبی به طرف دیگر معادله حاصل شده است. این تعریف میتواند به دیگر ضرب های تانسوری ( بسط داده شود. هنگامی که یک تبدیل مختصات انجام می دهیم، متعاقباْ تانسورها نیز به کمک ژاکوبی
بسط داده شود. هنگامی که یک تبدیل مختصات انجام می دهیم، متعاقباْ تانسورها نیز به کمک ژاکوبی 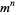 مولفه دارد که از قوانین تبدیلات مختصاتی پیروی می کند.
مولفه دارد که از قوانین تبدیلات مختصاتی پیروی می کند.
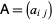 )، به جز اینکه یک تانسور مثلا
)، به جز اینکه یک تانسور مثلا 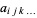 ،
، 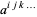 ،
، 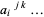 قدرت انتخاب هر تعداد شاخص دلخواه را شامل هستند. بعلاوه، یک تانسور از مرتبه ی
قدرت انتخاب هر تعداد شاخص دلخواه را شامل هستند. بعلاوه، یک تانسور از مرتبه ی  ،از نوع مختلط ـ شاخص یا به اصطلاح "مختلط"
،از نوع مختلط ـ شاخص یا به اصطلاح "مختلط"  ، تلفیقی از
، تلفیقی از  شاخص بالا یا "پادوردا (contravariant)" و
شاخص بالا یا "پادوردا (contravariant)" و  شاخص پایین "هم وردا (covariant)" می باشد. دقت کنید که مکان شاخص های پادوردا و هم وردا با یکدیگر فرق دارد که کوچکترین تفاوت میان جایدهی شاخص ها در یک تانسور چه در ترتیب و چه در بالا یا پایین بردن شاخص ها، منجر به ایجاد تانسور جدید و یا تغییر ساختمان ریاضی آن می گردد. برای مثال تانسور
شاخص پایین "هم وردا (covariant)" می باشد. دقت کنید که مکان شاخص های پادوردا و هم وردا با یکدیگر فرق دارد که کوچکترین تفاوت میان جایدهی شاخص ها در یک تانسور چه در ترتیب و چه در بالا یا پایین بردن شاخص ها، منجر به ایجاد تانسور جدید و یا تغییر ساختمان ریاضی آن می گردد. برای مثال تانسور  است.
است.  به شکل
به شکل  نوشته می شود. به طوریکه i=1,...,m و ماتریس متناظر با آن گویای تانسوری از مرتبه ی (۱,۱) است که آن را به فرم
نوشته می شود. به طوریکه i=1,...,m و ماتریس متناظر با آن گویای تانسوری از مرتبه ی (۱,۱) است که آن را به فرم  می نویسیم.
می نویسیم. ،
،  ،
،  و ... به دست آورد.
و ... به دست آورد.