در آنالیز مختلط گاهی با رابطه ای موسوم به رابطه ی اویلر سروکار داریم. (Trott 2004, p. 174) شکل کلی این رابطه به فرم معادله ی زیر است:

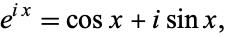
که در این معادله i واحد موهومی (imaginary unit) می باشد. عبارت هم ارز

ix=ln(cosx+isinx)

سابقاْ توسط کتس (Cotes) در سال ۱۷۱۴ میلادی به اثبات رسیده بود. حالت خاص فرمول فوق زمانی است که x=pi باشد. در این صورت شکل جالبی از فرمول فوق به صورت

e^(ipi)+1=0,

به دست می آید. زیبایی این رابطه با برقراری ارتباط میان اعداد بنیادی پی، e و i و عدد ۱ و ۰ و نیز عملگرهای بنیادی + و  × است که در عین سادگی بدلیل کارایی حیاتی آن در آنالیز فوریه (رجوع شود به این لینک)، یکی از زیباترین روابط شناخته شده در ریاضیات است. سادگی و اهمیت این رابطه از زبان گائوس نقل شده است: «اگر این رابطه بلافاصله در ذهن خواننده روشن نباشد، وی هرگز یک ریاضیدان طراز اول نخواهد شد.» (Derbyshire 2004, p. 202).

فرمول اویلر با استفاده از بسط یک سری به شکل زیر اثبات می شود:

sum_(n=0)^(infty)((ix)^n)/(n!)   =  e^(ix)            

sum_(n=0)^(infty)((-1)^nx^(2n))/((2n)!)+isum_(n=1)^(infty)((-1)^(n-1)x^(2n-1))/((2n-1)!)   =                  

cosx+isinx.  =                  

همچنین این رابطه از طریق انتگرال گیری مختلط هم قابل اثبات است. با در نظر گرفتن

 costheta+isintheta = z                

(-sintheta+icostheta)dtheta = dz              

i(costheta+isintheta)dtheta =                

izdtheta =                   

intidtheta =int(dz)/z          

itheta, = lnz             

بنابراین:

 e^(itheta) = z                

costheta+isintheta. =                  

منابع:

Castellanos, D. "The Ubiquitous Pi. Part I." Math. Mag. 61, 67-98, 1988.

Conway, J. H. and Guy, R. K. "Euler's Wonderful Relation." The Book of Numbers. New York: Springer-Verlag, pp. 254-256, 1996.

Cotes, R. Philosophical Transactions 29, 32, 1714.

Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, 2004.

Euler, L. Miscellanea Berolinensia 7, 179, 1743.

Euler, L. Introductio in Analysin Infinitorum, Vol. 1. Lausanne, p. 104, 1748.

Hoffman, P. The Man Who Loved Only Numbers: The Story of Paul Erdos and the Search for Mathematical Truth. New York: Hyperion, p. 212, 1998.

Trott, M. The Mathematica GuideBook for Programming. New York: Springer-Verlag, 2004.