تانسورها
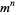مولفه دارد که از قوانین تبدیلات مختصاتی پیروی می کند.
هر شاخص تانسور، فقط مقادیری در محدوده ی تعداد بعدهای فضای تعریفی اختیار می کند. با این حال دخالت ابعاد فضایی تا حدود زیادی در معادلات تانسوری نامربوط به نظر می رسد. (به استثنای حالت تنجش یافته ی تانسور کرونکر). تانسورها نوع عمومی تر اسکالرها ( که فاقد شاخص هستند) ،بردارها (که تنها دارای یک شاخص اند) و نیز متریک ها (که فقط دو شاخص دارند) می باشند که می توانند تعداد دلخواه شاخص اختیار کنند.
تانسورها بستر ریاضی مناسب و ساده ای را جهت فرمولبندی و حل مسائل متعدد در سیطره ی مباحث گوناگون فیزیک نظیر مکانیک سیالات و نسبیت عام فراهم می کنند.
نمادگذاری هر تانسور عیناْ شبیه به یک ماتریس است، (مثل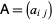 
)، به جز اینکه یک تانسور مثلا 
، 
، 
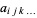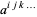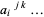قدرت انتخاب هر تعداد شاخص دلخواه را شامل هستند. بعلاوه، یک تانسور از مرتبه ی 
،از نوع مختلط ـ شاخص یا به اصطلاح "مختلط" 
، تلفیقی از 
شاخص بالا یا "پادوردا (contravariant)" و 
شاخص پایین "هم وردا (covariant)" می باشد. دقت کنید که مکان شاخص های پادوردا و هم وردا با یکدیگر فرق دارد که کوچکترین تفاوت میان جایدهی شاخص ها در یک تانسور چه در ترتیب و چه در بالا یا پایین بردن شاخص ها، منجر به ایجاد تانسور جدید و یا تغییر ساختمان ریاضی آن می گردد. برای مثال تانسور 
متمایز از شکل 
است.
هنگامی که تانسور نسبت به تفاوت شاخص های پادوردا و هم وردا حساس باشد، تانسور حاصل از نوع عمومی خواهد بود. (در بحث ماتریس ها، یک ماتریس عمومی از جمع دو ماتریس پادمتقارن و متقارن به وجود می آمد که در اینجا نیز همین حالت برای تانسورها برقرار است). عدم تفاوت میان شاخص های هم وردا و پادوردا بیشتر در تانسورهای موردبحث در فضای اقلیدسی مانند تانسورهای دکارتی (Cartesian tensors) مطرح است.
تانسورهای تبدیل شونده از مرتبه ی صفر، اسکالر (scalars) نامیده می شوند که همانند تانسورهای مرتبه ی ۱ یعنی بردارها (vectors) تبدیل می شوند. در نمادنویسی تانسوری، هر بردار 
به شکل 
نوشته می شود. به طوریکه i=1,...,m و ماتریس متناظر با آن گویای تانسوری از مرتبه ی (۱,۱) است که آن را به فرم 
می نویسیم.
می توان عملیات جبری و دیفرانسیل را بر روی تانسورها انجام داد (مانند تانسورهای متریک (metric tensors) و تانسور جایگشت (permutation tensor) یا نماد دلتای کرونکر) که قابلیت تعریف پذیری عملگرهای تانسوری را دارا هستند. [مانند مشتق هم وردا (semicolon derivatives)]. با جابجایی شاخص های هم وردا و پادوردا می توان به عبارات و تانسورهای ساده تری دست یافت که این کار شامل بالابردن (index raising) یا پایین آوردن شاخص ها (index lowering) یا به عبارت کلی بالانس شاخص ها ( index gymnastics) می باشد که آن ها را می توان با ضرب در تانسور متریک، 
، 
، 
و ... به دست آورد.
ادامه دارد...
منابع:
Abraham, R.; Marsden, J. E.; and Ratiu, T. S. Manifolds, Tensor Analysis, and Applications, 2nd ed. New York: Springer-Verlag, 1991.
Akivis, M. A. and Goldberg, V. V. An Introduction to Linear Algebra and Tensors. New York: Dover, 1972.
Arfken, G. "Tensor Analysis." Ch. 3 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 118-167, 1985.
Aris, R. Vectors, Tensors, and the Basic Equations of Fluid Mechanics. New York: Dover, 1989.
Bishop, R. and Goldberg, S. Tensor Analysis on Manifolds. New York: Dover, 1980.
Borisenko, A. I. and Tarpov, I. E. Vector and Tensor Analysis with Applications. New York: Dover, 1980.
Bott, R. and Tu, L. W. Differential Forms in Algebraic Topology. New York: Springer-Verlag, 199.
Cartan, É. The Theory of Spinors. New York: Dover, 1981.
Joshi, A. W. Matrices and Tensors in Physics, 3rd ed. Wiley, 1995.
Lass, H. Vector and Tensor Analysis. New York: McGraw-Hill, 1950.
Lawden, D. F. An Introduction to Tensor Calculus, Relativity, and Cosmology, 3rd ed. Chichester, England: Wiley, 1982.
Lovelock, D. and Rund, H. Tensors, Differential Forms, and Variational Principles. New York: Dover, 1989.
McConnell, A. J. Applications of Tensor Analysis. New York: Dover, 1947.
Nicolaescu, L. I. Lectures on the Geometry of Manifolds. Singapore: World Scientific, 1996.
Parker, L. and Christensen, S. M. MathTensor: A System for Doing Tensor Analysis by Computer. Reading, MA: Addison-Wesley, 1994.
Rashevskii, P. K. Riemann'sche Geometrie und Tensoranalysis. Berlin: Deutscher Verlag der Wissenschaften, 1959.
Simmonds, J. G. A Brief on Tensor Analysis, 2nd ed. New York: Springer-Verlag, 1994.
Sokolnikoff, I. S. Tensor Analysis: Theory and Applications to Geometry and Mechanics of Continua, 2nd ed. New York: Wiley, 1964.
Synge, J. L. and Schild, A. Tensor Calculus. New York: Dover, 1978.
Wrede, R. C. Introduction to Vector and Tensor Analysis. New York: Wiley, 1963